Modeling in one material (e.g. p/n diode, resistor)

Work in Progress...

Set up governing differential equations in the material:

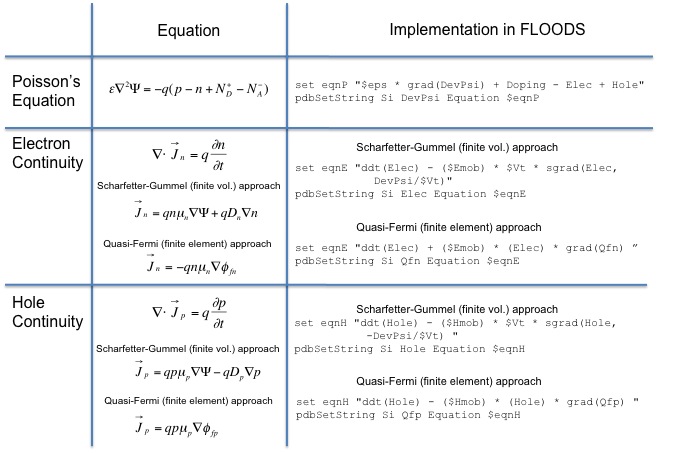
For semiconductors, the basic equations that describe transport of electrons and holes and electrostatic potential are the continuity equations for electrons and holes and the Poisson Equation as given in the table below. Other differential equations such as the heat equation could also be included in the model.

The tcl/alagator scripts for the corresponding differential equations are given in the table, where"eso" is <math>\epsilon_0\epsilon_r/q</math>, "Emob" and "Hmob" are the electron and hole mobilities, and "Vt" is <math>kT/q</math>. One of two approaches may be used to implement the continuity equations (Scharfetter-Gummel or Quasi-Fermi), which use either finite volume or finite element methods, respectively.

Designate solution variables:

If the Sharfetter-Gummel approach is used then the solution variables will be <math>\Psi</math>, n, and p or "DevPsi", "elec", and "hole". They are implemented in FLOODS as follows.

solution add name=DevPsi solve negative damp
solution add name=Elec solve !negative
solution add name=Hole solve !negative

It is useful to define the Quasi Fermi potentials for later use in contact boundary conditions or plotting.

term name=Qfp add silicon eqn = "DevPsi + $Vt*log(Hole/$ni)"
term name=Qfn add silicon eqn = "DevPsi - $Vt*log(Elec/$ni)"

If the Quasi-Fermi approach is used, then the solution variables will be <math>\Psi</math>, <math>\Phi_{fn}</math>, and <math>\Phi{fp}</math> or "DevPsi", "Qfn", and "Qfp" implemented in FLOODS as follows. In this case, elec and hole need to be defined as a constant solution variable.

solution add name=DevPsi solve negative damp
solution add name=Elec const solve val= "$ni*exp((DevPsi-Qfn)/$Vt)+1.0"
solution add name=Hole const solve val= "$ni*exp((Qfp-DevPsi)/$Vt)+1.0"
solution add name=Qfp solve negative damp
solution add name=Qfn solve negative damp

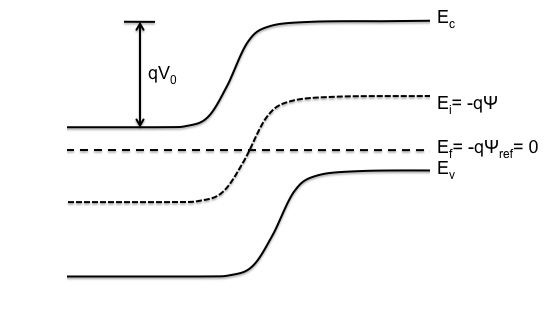
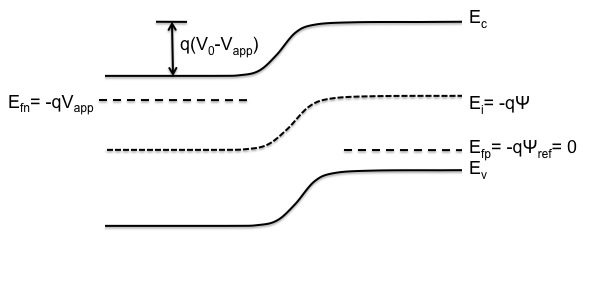
Determine where the reference potential is

Give Boundary Conditions:

Give Initial Conditions: