Resistor example 1D - Initial conditions explanation
This page explains the following code snipped from the 1D Resistor example:
Initial conditions
#Bias Voltage on the Contacts contact name=VSS voltage supply=0.0 contact name=GND voltage supply=0.0 #Initial Guess at Zero Bias sel z=(-$Vt*log(-($Doping+$small)/$ni)) name=DevPsi sel z=$ni*exp(DevPsi/$Vt) name=Elec sel z=$ni*exp(-DevPsi/$Vt) name=Hole #DC Solve at Zero Bias device
Why Always Start at Zero Volts?
The first 2 floods lines are how to put a voltage on any floods contact:
contact name=VSS voltage supply=0.0 contact name=GND voltage supply=0.0
The 0.0 is in Volts. The purpose of always starting or doing an initial solve with 0V on all contacts is because 0V is usually boring - it's easy to guess what the Fermi levels are doing, and therefore what DevPsi, Elec, and Hole are.
Initial Guess Physics
The next 3 floods lines is the initial guess we're using for our 3 pde variables.
We start (again) with the Maxwell-Boltzmann (MB) equation for electron concentration:
<math>n=ni*exp(\frac{E_{fn}-E_i}{kT})</math>
We guess that, at zero-bias, the fermi levels are zero, and we assign DevPsi = Ei. This gives us
<math>n=ni*exp(\frac{0-\Psi}{kT})</math>
Solving for DevPsi:
<math>\Psi=-kT*log(\frac{n}{ni})</math>
One further step, to make the expression for DevPsi consist of entirely known quantities, we say that n=Nd, which for us, is approximately equal to the total Doping, since Nd>>Na:
<math>\Psi=-kT*log(\frac{Nd}{ni})</math> or <math>\Psi=-kT*log(\frac{Doping}{ni})</math>
In floods, this initial guess for Psi is expressed via
sel z=(-$Vt*log(-($Doping+$small)/$ni)) name=DevPsi
What does sel z= actually do?
When floods executes this "sel z=" command, it parses and solves the equation after the "=" immediately, on each grid point, and saves those values in a table under the name after the "name=". In the case for the DevPsi initial guess:
sel z=(-$Vt*log(-($Doping+$small)/$ni)) name=DevPsi
all the arguments in the equation string
(-$Vt*log(-($Doping+$small)/$ni))
are simple numbers. In this case, "sel z=" evaluates that number (does the math), and puts that number on each grid point with the name "DevPsi."
For the case of the Elec and Hole initial guesses:
sel z=$ni*exp(DevPsi/$Vt) name=Elec sel z=$ni*exp(-DevPsi/$Vt) name=Hole
the "sel z=" solves the expression at each grid point using the unique DevPsi from that grid point.
In other words, "sel z=" is what you use when you have a variable (Elec, Hole, or DevPsi in this case) that exists on all grid points, and therefore depends on what x, y, and z coordinates it is at. This might not be clear here because we have only a 1D structure, and at the moment DevPsi is the same number at every grid point. Here is a mental picture you can use to think of what "sel z=" is doing. First, remember the 1D grid you plotted in your "init" steps:
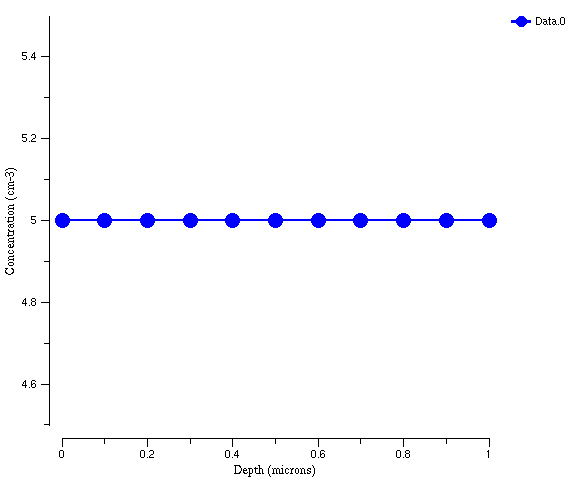
Now imagine that at each dot, or grid point, in the picture is a little box - a separate one for each variable (i.e. on each grid point there is 1 box for DevPsi, 1 box for Elec, and 1 box for Hole). When you say "sel z=", floods evaluates the expression after the "=" and places the answer in each box. For example, if you did:
sel z=5 name=FavoriteNumber
then floods would create a new box on each grid point called "FavoriteNumber" and put 5 in the boxes. We'll revisit this in the 1D diode example, in which the doping will have to depend on x. You can imagine also that all these boxes are actually somewhere in the parameter database (since floods is not drawing a mental picture for itself).
the "device" command
The "device" command is what actually tells floods to start solving your 3 pde equations. When floods encounters this command, it parses the pdb and gets all the Equation strings and initial conditions it needs, and then does an iterative DC solve starting with the initial guess you gave it. You'll see output printed to your screen like this:
device
Iter Time L S Sparse 2Norm Update
1 0.00000e+00 0.00000e+00 1.51024e-16 1.88193e+02 3.12757e-03
2 1.00000e-02 0.00000e+00 4.32083e-22 1.25462e+02 2.08503e-03
3 0.00000e+00 0.00000e+00 8.10156e-23 8.36415e+01 1.39001e-03
4 0.00000e+00 0.00000e+00 1.27426e-16 5.57610e+01 9.26667e-04
Solution time 1.00000e-02
Total Device Solution Time 1.00000e-02
"Iter" stands stands for iteration - in this case it took floods 4 tries to reach convergence (a solution sufficiently near the guess). The last column, "Update," shows how much the floods error changed from the last iteration (0 error is best). If you remember, we set the maximum tolerable error with the Abs.Error and Rel.Error booleans in the pdb.