Resistor example 1D - Initial conditions explanation
This page explains the following code snipped from the 1D Resistor example:
Initial conditions
#Bias Voltage on the Contacts contact name=VSS voltage supply=0.0 contact name=GND voltage supply=0.0 #Initial Guess at Zero Bias sel z=(-$Vt*log(-($Doping+$small)/$ni)) name=DevPsi sel z=$ni*exp(DevPsi/$Vt) name=Elec sel z=$ni*exp(-DevPsi/$Vt) name=Hole #DC Solve at Zero Bias device
Why Always Start at Zero Volts?
The first 2 floods lines are how to put a voltage on any floods contact:
contact name=VSS voltage supply=0.0 contact name=GND voltage supply=0.0
The 0.0 is in Volts. The purpose of always starting or doing an initial solve with 0V on all contacts is because 0V is usually boring - it's easy to guess what the Fermi levels are doing, and therefore what DevPsi, Elec, and Hole are.
Initial Guess Physics
The next 3 floods lines is the initial guess we're using for our 3 pde variables.
We start (again) with the Maxwell-Boltzmann (MB) equation for electron concentration:
<math>n=ni*exp(\frac{E_{fn}-E_i}{kT})</math>
We guess that, at zero-bias, the fermi levels are zero, and we assign DevPsi = Ei. This gives us
<math>n=ni*exp(\frac{0-\Psi}{kT})</math>
Solving for DevPsi:
<math>\Psi=-kT*log(\frac{n}{ni})</math>
One further step, to make the expression for DevPsi consist of entirely known quantities, we say that n=Nd, which for us, is approximately equal to the total Doping, since Nd>>Na:
<math>\Psi=-kT*log(\frac{Nd}{ni})</math> or <math>\Psi=-kT*log(\frac{Doping}{ni})</math>
In floods, this initial guess for Psi is expressed via
sel z=(-$Vt*log(-($Doping+$small)/$ni)) name=DevPsi
What does sel z= actually do?
When floods executes this "sel z=" command, it parses and solves the equation after the "=" immediately, on each grid point, and saves those values in a table under the name after the "name=". In the case for the DevPsi initial guess:
sel z=(-$Vt*log(-($Doping+$small)/$ni)) name=DevPsi
all the arguments in the equation string
(-$Vt*log(-($Doping+$small)/$ni))
are simple numbers. In this case, "sel z=" evaluates that number (does the math), and puts that number on each grid point with the name "DevPsi."
For the case of the Elec and Hole initial guesses:
sel z=$ni*exp(DevPsi/$Vt) name=Elec sel z=$ni*exp(-DevPsi/$Vt) name=Hole
the "sel z=" solves the expression at each grid point using the unique DevPsi from that grid point.
In other words, "sel z=" is what you use when you have a variable (Elec, Hole, or DevPsi in this case) that exists on all grid points, and therefore depends on what x, y, and z coordinates it is at. This might not be clear here because we have only a 1D structure, and at the moment DevPsi is the same number at every grid point. Here is a mental picture you can use to think of what "sel z=" is doing. First, remember the 1D grid you plotted in your "init" steps:
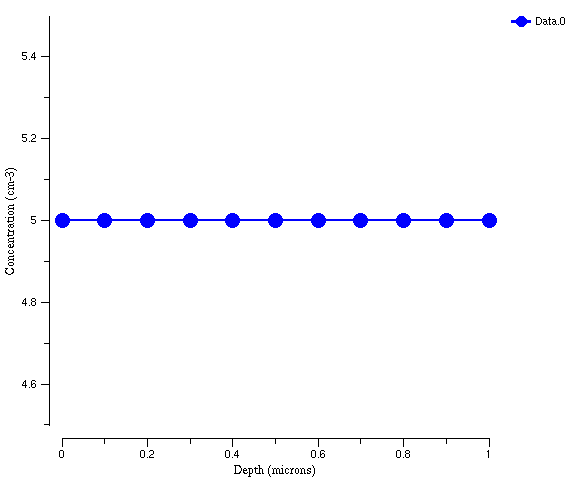
Now imagine that at each dot, or grid point, in the picture is a little box - a separate one for each variable (i.e. on each grid point there is 1 box for DevPsi, 1 box for Elec, and 1 box for Hole). When you say "sel z=", floods evaluates the expression after the "=" and places the answer in each box. For example, if you did:
sel z=5 name=FavoriteNumber
then floods would create a new box on each grid point called "FavoriteNumber" and put 5 in the boxes. We'll revisit this in the 1D diode example, in which the doping will have to depend on x.