Device Solves: Difference between revisions
Jump to navigation
Jump to search
| Line 14: | Line 14: | ||
==Sinusoidal Steady State Analysis== | ==Sinusoidal Steady State Analysis== | ||
Consider the symbolic representation of the 3 device equations: Poisson, electron and hole continuity equations. | Consider the symbolic representation of the 3 device equations: Poisson, electron and hole continuity equations. | ||
[[File:Dev_eqn.png]] | [[File:Dev_eqn.png|200px]] | ||
This technique solves the device equation system in the frequency domain as a steady state perturbed by an infinitesimal signal. The small signal assumption allows linearization of the device around the DC bias point. Consequently the AC system can then be defined in the form: [J+jD]X=B where D contains the time dependent element of the continuity equations. For computational reasons, the AC system takes the form of equation [4], where D is now a diagonal matrix with ω=2πf as its diagonal elements, and XR and XI are real and imaginary components of the solution variables. | This technique solves the device equation system in the frequency domain as a steady state perturbed by an infinitesimal signal. The small signal assumption allows linearization of the device around the DC bias point. Consequently the AC system can then be defined in the form: [J+jD]X=B where D contains the time dependent element of the continuity equations. For computational reasons, the AC system takes the form of equation [4], where D is now a diagonal matrix with ω=2πf as its diagonal elements, and XR and XI are real and imaginary components of the solution variables. | ||
Revision as of 17:47, 5 January 2016
FLOODS Specific Commands
- Initial Guess - start the numerical solve off well
- contact - define contacts physically, and define contact physics
- device - bias contacts and solve steady-state or transient
Steady-State
Transient
Frequency domain
Sinusoidal Steady State Analysis
Consider the symbolic representation of the 3 device equations: Poisson, electron and hole continuity equations.
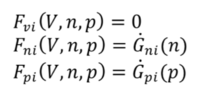This technique solves the device equation system in the frequency domain as a steady state perturbed by an infinitesimal signal. The small signal assumption allows linearization of the device around the DC bias point. Consequently the AC system can then be defined in the form: [J+jD]X=B where D contains the time dependent element of the continuity equations. For computational reasons, the AC system takes the form of equation [4], where D is now a diagonal matrix with ω=2πf as its diagonal elements, and XR and XI are real and imaginary components of the solution variables.